| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- YOLO
- coding
- image
- FunctionGemma
- 영화
- 딥러닝
- lightly
- 파이썬
- llm
- Fultter
- Flutter
- docker
- Gemma
- Ai
- DART
- chatGPT
- Kubernetes
- ultralytics
- container
- 구글
- Type
- 인공지능
- 야호
- 엔지니어
- 리뷰
- Python
- clone
- GenAI
- 클론코딩
- 논문리뷰
- Today
- Total
딥러닝 공부방입니다. 근데 이제 야매를 곁들인.
[논문리뷰] Unsupervised Learning of Visual Representations by Solving Jigsaw Puzzles 본문
[논문리뷰] Unsupervised Learning of Visual Representations by Solving Jigsaw Puzzles
ZeroAct 2021. 12. 5. 04:22오늘은 transfer learning을 위한 사전학습을 하는 아이디어를 제안한 논문을 살펴 보겠습니다.

이런 퍼즐 아시죠? 모델이 이 Jigsaw Puzzle 문제를 풀도록 학습하는 것이 사전학습에 도움이 된다고 합니다.
2017년에 나온 비교적 오래된 논문이지만 아이디어가 재밌어서 읽게 되었습니다.
1 Abstract. 2 Introduction.
저자는 self-supervision을 원칙을 따라 Jigsaw puzzle을 푸는 모델을 학습함으로써 이 모델을 다른 목적에 맞게 repurpose 할 수 있다고 합니다.
여기서 self-supervision은 레이블링이 필요 없다는 말이고 repurpose는 전이학습을 의미합니다.
이 방식으로 사전학습을 하는 것이 AlexNet보다 파라미터 수도 적으면서 semantic learning capabilities를 유지할 수 있다고 합니다. 파라미터 수가 적은데 모델의 성능은 줄지 않았다 정도로 이해하시면 될 것 같습니다.
3 Related Work.
일단 이 논문이 뭘 하려는지 알기 위해서는 representation/feature learning이 무엇인지 알면 좋을 것 같습니다.
제 방식으로 설명 드리자면,
보통 이미지 분류나 객체 탐지 모델을 학습하기 위해서는 정답, 즉, 노동이 필요합니다.
직접 레이블링을 해보신 분들은 알겠지만 정말 딥러닝 서비스를 배포하는 모든 과정중에 제일 고된 작업입니다.
이 노동을 줄이기 위한 방법 중에는 representation/feature learning 을 통한 사전학습이 있습니다.
고양이와 개를 분류하는 문제를 아무것도 모르는 모델을 가지고 처음부터 학습하는 것보다는 눈의 모양이나 귀의 모양을 캐치해 낼 수 있는 모델을 가지고 학습하는 것이 당연히 쉽겠죠.
그런 방법입니다.
논문에서 a natural choice is the goal of disentangling factors of variation 이라는 말이 있습니다.
Unsupervised Learning을 할 때 일반적으로 좋은 기준을 학습하라고 설계할 수는 없지만 결국 다양한 특징 요소들을 잘 disentangling 하는 것이 좋다는게 당연하다는 말입니다.
저자는 Jigsaw Puzzle을 푸는 모델을 이러한 특징들을 잘 분리하도록 설계했다고 합니다.
Abstract. 에서 논문에서 제안하는 모델을 Unsupervised가 아닌 Self-supervision을 따른다고 했는데 사진만 있으면 정답 데이터를 스스로 만들어 낼 수 있는 문제이기 때문에 사실상 정답이 있는 문제이기 때문입니다.
뒤에 설명이 나오겠지만 이 논문은 Jigsaw Puzzle 문제를 어렵게 만들기 위한 여러가지 꼼수를 사용합니다.
이 때문에 모델은 다른 tile들 간의 유사성을 무시하고, 차이에 집중한다고 합니다.
그래서 하얀 자동차들만 가지고 학습을 해도 검은 자동차에 대한 문제를 풀 수 있게 됩니다.
3 Solving Jigsaw Puzzles
(갑자기 여기부터 반말모드...)
이 파트에서 하고자 하는 말을 요약하면,
Jigsaw Puzzle 문제를 쉽게 만드는 shortcut(편법)으로 사용될 수 있는 요소들을 최대한 다 제거해서 각 tile(퍼즐 한 조각)의 특징만을 사용해서 문제를 풀도록 설계하였다.

이 호랑이 문제가 있을 때 무늬라던가 색이라던가 테두리라던가 바위 패턴이라던가 이런 shortcut들이 있으면 그것만 보고 맞출 수 있기 때문에 진짜 목적인 representation/feature learning이 이루어지지 않을 수 있다.
그래서 여러가지 제약을 걸어 이 tile은 얼굴, 이 tile은 다리, 이 tile은 몸통, 즉, 각 tile의 특징만으로 문제를 풀도록 설계했다.
3.1 The Context-Free Architecture.
이러한 shortcut들을 방지하기 위한 방법중 첫 번째로 Context-Free Network 이하 CFN를 제안한다.
context라는 말은 직역하면 문맥이라는 말인데 Jigsaw Puzzle 문제에서 문맥은 각 tile간의 관계를 의미한다.
앞서, 각 tile의 특징만으로 문제를 풀도록 설계했다고 했는데, 만약 모델이 각 tile간의 상관관계를 파악할 수 있는 여지를 준다면 아무리 제약을 걸어도 Context-Free를 달성하기 힘들 것이다.
저자는 Context-Free를 달성하기위해 다음과 같은 구조를 사용했다.
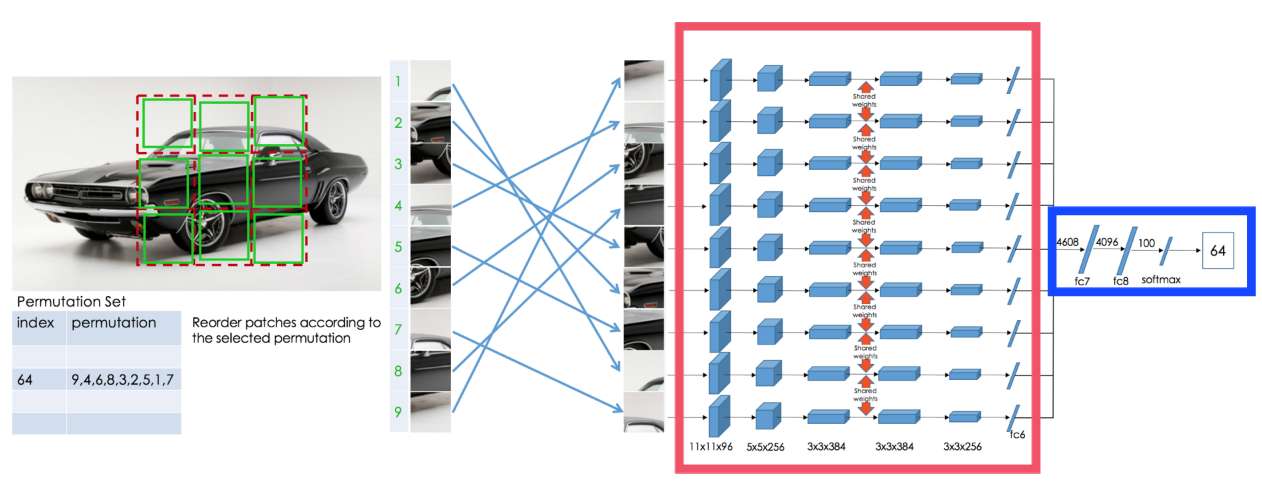
빨간 box안의 모델은 AlexNet 구조를 그대로 사용했으며 특징을 학습하는 구간이다.
이 구간에서는 모든 tile이 따로 forward 되기 때문에 어떠한 관계도 생기지 않는다.
파란 box까지 가고 나서야 비로소 각 tile들의 특징들을 합쳐지게 되어 관계가 생긴다.
저자는 이 전략을 delays the computation of statistics across different tiles라고 표현했다.
3.2 The Jigsaw Puzzle Task
Jigsaw Puzzle 문제는 tile 갯수가 9개 이기 때문에 9! = 362880개의 문제를 만들 수 있다.
근데 모든 경우의 수를 학습하기 보다는 미리 정해놓은 몇개의 permutation을 저장해 놓고 모델이 입력으로 들어온 tile들의 순서가 몇 번째 index의 permutation과 일치하는지를 맞추도록 학습했다.
뒤에서 다루겠지만 이 permutation set을 어떻게 정하는지가 representation learning의 성능에 큰 영향을 미친다고 한다.
3.3 Training the CFN
다시 강조하지만 이 논문이 하고자 하는 것은 전이학습을 위한 사전학습이다.
CFN을 아무런 제약 없이 그냥 학습하면 진짜 목적인 이미지 분류, 객체 탐지 등으로의 전이학습을 위한 특징이 아닌 Jigsaw Puzzle만을 풀기위한 특징을 학습하게 된다.
Jigsaw Puzzle만을 풀기위한 특징으로 tile의 위치 자체, edge continuity(테두리가 이어지는 것), pixel/color intensity(색), chromatic aberration(색수차; 카메라의 문제나 촬영 환경에 의해 색이 이상하게 나오는것)등이 있다. 저자는 이를 shortcut이라고 부른다.
이러한 shortcut들을 제거하기 위해 다양한 방법들을 사용하는데 ablation study에서 다룬다.
4. Experiments
4.1 Transfer Learning
전이학습!
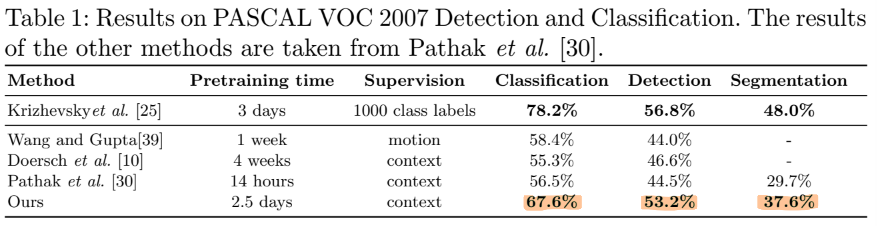
PASCAL VOC 2007 Dataset에 적용한 결과인데 보시다시피 이당시 기법들중 제일 좋다.
눈여겨 볼것은 성능도 1등이지만 Pretraining time 조차도 짧은 편이라는 것이다.
사전 연구중에 transfer learning을 할 때 마지막 Layer가 사전학습을 할때 사용한 데이터와 목적에 특화되어 있다는 사실이 밝혀진 적이 있다.
저자는 ImageNet 2012 Dataset으로 실험을 하면서 이를 검증해 봤는데 전이 학습시 모든 Conv Layer 가중치를 그대로 두었을 때 34.6%의 성능이 나왔지만 마지막 conv layer인 conv5를 같이 학습하니 45.3%로 상당한 성능 향상이 있었다.
conv4, conv3, conv2, conv1을 같이 학습했을때는 성능향상이 비교적 적은 편이다.
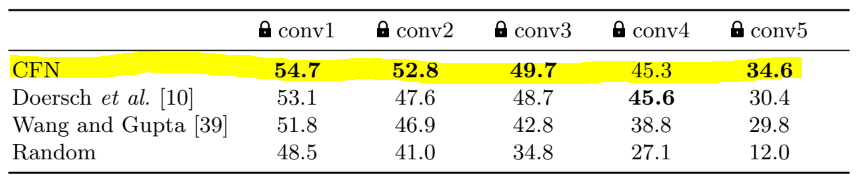
이것이 CFN 마저도 마지막 Layer인 conv5가 Jigsaw Puzzle문제를 푸는데 특화되어있다는 것을 보여준다.
4.2 Ablation Study
저자가 Ablation Study에서 하고자 하는 말은 이거다.
A good self-supervised task is neither simple nor ambiguous.
좋은 self-supervised 사전학습 문제는 간단하지도 모호하지도 않다.
Permutation Set.
Jigsaw Puzzle 문제의 정답인 permutation set을 만들 때 다음을 고려했다고 한다.
1) Cardinality
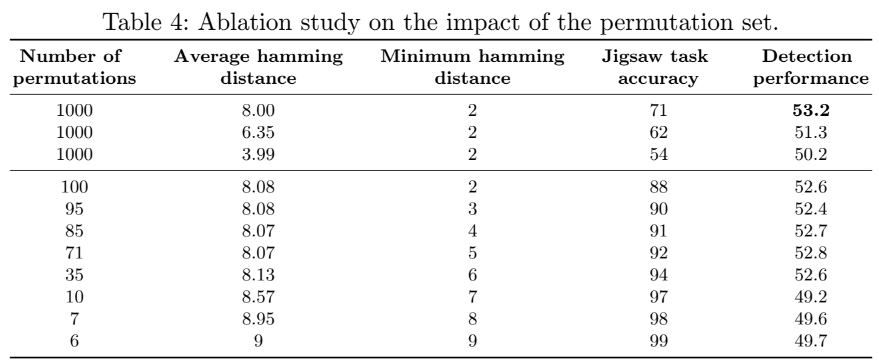
permutation set의 수가 많을 수록 Jigsaw Puzzle의 정확도는 낮아지지만 전이학습의 성능은 좋아졌다.
2) Average Hamming distance
Hamming distance는 집합 사이의 거리를 나타내는 지표중 하나로 예시를 들면 다음과 같다.
{1 2 3 4}와 {1 3 2 4}사이의 Hamming distance는 2이다. 두번째 세번째 요소가 다르기때문.
직관적으로 평균 Hamming distance가 크면 비슷한 permutation이 적으므로 tile이 비슷한 순서로 나열되는 경우가 줄어들것이고 이는 training set에 과적합 되는 것을 막을 수 있게 될 것이다.
결과적으로 Hamming distance가 클 수록 Jigsaw Puzzle의 정확도와 전이학습의 성능이 좋아졌다.
3) Minimum hamming distance
100개로 시작해서 최소 hamming distance 값을 조정하며 갯수를 조정해보았다. 당연히 값이 커질 수록 갯수가 줄어들고 Jigsaw Puzzle이 쉬워지지만 전이학습 성능은 떨어진다.
Preventing Shortcuts.
3.3 에서 언급한 edge continuity, pixel/color intensity, chromatic aberration은 단순한 trick이니 간단히 설명하면 tile을 자를 때 그대로 자르지 않고 여백을 주고 자르고, tile마다 다르게 normalize를 해주고, gray 이미지 color 이미지를 3대 7로 섞어서 학습한다.

역시 셋다 하는 것이 가장 좋다.
4.3 4.4
Jigsaw Puzzle을 풀도록 학습된 특징이 전이학습에 좋다는 것을 반복해서 언급한다.
후기
논문을 많이 읽어왔지만 직접 리뷰를 작성해보니 참 힘든 일 인것 같습니다...
단순한 논문이라고 생각했는데 리뷰를 작성하려고 하니 시간이 상당히 많이 걸렸네요.
첫 리뷰라 많이 서투른데 지적 해주세요. 감사합니다!
ps. 논문리뷰 블로거 분들에게 경의를 표합니다.




